Kinematic Approach

An alternative to the computational expensive physically-based approach, could be to use a kinematics approach. The large majority of research in this area has focused on gait generation, and therefore involves the lower half of the body and in particular deals with the sagittal elevation angle.

"The Sagittal Plane is a vertical plane which bisects the figure into left and right halves. We define a limb segment v between two points a and b on the limb: v = a - b. Typically a and b are points at opposite ends of a limb, e.g. the knee centre and the ankle centre are used to measure the elevation of the lower leg. We project v onto the sagittal plane to form v(sag). The angle between v(sag) and the negative y axis is its sagittal elevation angle." Sun & Metaxas (2001).

 

Measuring the pelvis sagittal elevation angle

 

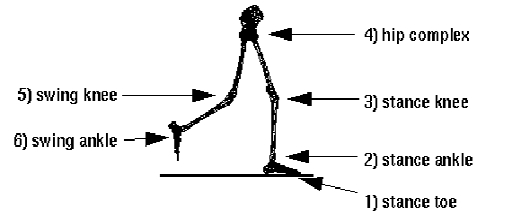
Although there are different ways to calculate the motion depending on requirements and constraints, a common constraint is to have the standing foot make contact with the ground. Therefore, the character's root transformation is computed first and then the character's joint angles are calculated, starting with the stance leg and working round to the bottom of the swing leg. The diagram below illustrates the order of computation of the joint angles.

The joint angles and their order of computation, Sun & Metaxas (2001)

 

Harold Sum gives a good description of how his system (ElevWalker) works in this manner. He starts by describing how the rotation angles are calculated by the contact point and how this contact point continuously moves forward along the bottom of the foot, thus requiring the contact point to recalculated at each frame.

"Once we have the point of contact, we rotate the foot segment so that its orientation equals the dataset foot elevation angle. The rotation axis is a vector normal to the sagittal plane, and through the point of contact. By rotating about the axis, and by recomputing the point of contact at each frame, the foot stays on the surface of the ground and does not penetrate it. We define the foot being flat on the ground as occurring when a point in the forefoot (toe segments) and a point in the hindfoot (heel segment) are both in contact with the ground. When this condition is met, the root is moved to the toes, and the elevation of the foot is then satisfied by the first toe joint (allowing the heel to rise from the ground). The root transformation no longer changes until the swing side stance are swapped." H.Sun (2001).

The performance of the kinematic approach is highly dependent on the number of degrees of freedom (DOF) of the character. Lee & Shin, suggest that a reasonable human model may have about 40 DOF, but normally much fewer are specified when manipulating the model. For a figure of n DOFs, c of those can be removed with a set of c independent constraints imposed on it. The remaining (n - c) DOFs span the solution space of the problem. With this reduction of DOFs and the use of redundancy, as highlighted by Korein & Badler (1982), real-time animation is possible with the kinematic approach unlike the physically-based approach.

Top